[알고리즘] 이진 탐색(Binary Search)

이진 탐색(Binary Search)란?

오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다.

배열의 중간 값을 임의의 값 X로 선택하여, 찾고자 하는 값보다 크면 우측 데이터를 대상으로,

작으면 좌측 데이터를 대상으로 해당 값을 찾을 때 까지 반복하여 검색한다.

 

장점

• 목표 값을 찾을 확률이 두배가 되어 속도가 빠르다.

단점

• 정렬된 리스트에만 사용할 수 있다.

 

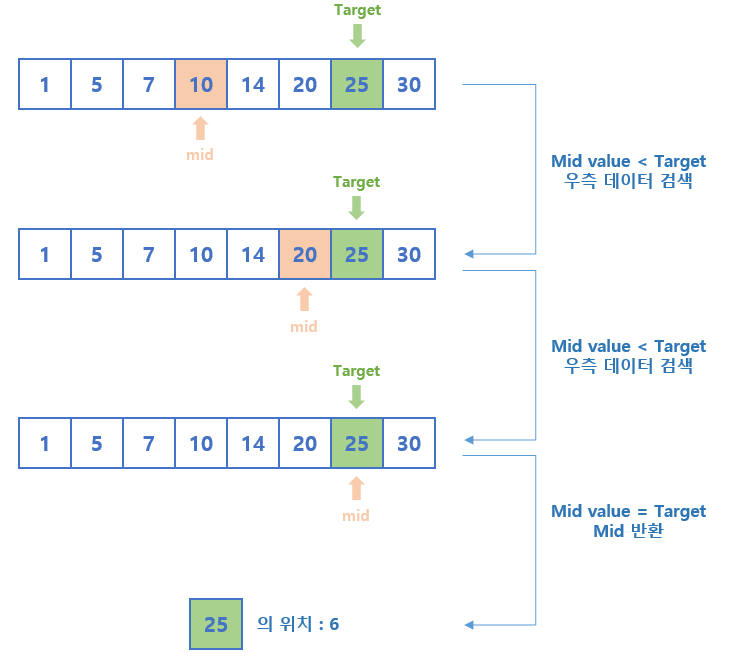
이진 탐색 과정

   1. 정렬된 리스트를 준비한다.

   2. 중간 지점을 찾는다. (left + right) / 2
   3. 중간 지점의 값과 목표하는 값을 비교한다.

       3.1 중간 지점의 값 < 목표하는 값의 경우

             - 검색 범위를 중간 지점의 우측으로 변경한다.

       3.2 중간 지점의 값 > 목표하는 값의 경우

             - 검색 범위를 중간 지점의 좌측으로 변경한다.
   4. 목표하는 값을 찾을 때 까지 반복한다. 

---

이진 탐색 그림

 

알고리즘 구현

반복문 방식

#include <iostream>
#include <vector>
using namespace std;

/*
 * 반복문 방식 이진 탐색
 */
int binarySearch(vector<int>& arr, int target){
    int left,right,mid;
    
    left = 0;
    right = arr.size() -1;
    
    while(left <= right){
        mid = (left + right) / 2;
        
        if(target < arr[mid]) 
            right = mid - 1;
        else if(target > arr[mid])
            left = mid + 1;  
        else
            return mid;
    }
    return -1;
}

int main(){
	//정렬된 리스트
    vector<int> arr = {1,3,4,5,6,7,8,10,15,46,54,66,100};
    
    int targetValue = 54;
    
    int index = binarySearch(arr,targetValue);
    
    cout << targetValue << " 의 위치 : " << index << endl;
    
    return 0;
}

재귀 방식

#include <iostream>
#include <vector>
using namespace std;

/*
 * 재귀 방식 이진 탐색
 */
int binarySearch(vector<int>& arr,int left,int right, int target){
    int mid = (left + right) / 2;
    
    if(arr[mid] == target)
        return mid;
    else if(arr[mid] < target)
        return binarySearch(arr,mid + 1,right,target);
    else if(arr[mid] > target)
        return binarySearch(arr,left,mid - 1,target);
        
    return -1;
}
int main(){
	//정렬된 리스트
    vector<int> arr = {1,3,4,5,6,7,8,10,15,46,54,66,100};
    
    int targetValue = 54;
    int left = 0;
    int right = arr.size() - 1;
    
    int index = binarySearch(arr,left,right,targetValue);
    
    cout << targetValue << " 의 위치 : " << index << endl;
    
    return 0;
}

시간 복잡도

• 절반씩 검색하여 목표하는 값을 찾아나간다.
• 평균 시간 복잡도 : O(log2 N)

 

---