퀵 정렬(Quick Sort)이란?
다른 원소와의 비교만으로 정렬을 수행하는 비교정렬에 속한다.
분할 정복 알고리즘 중 하나, 매우 빠른 수행속를 가지고 있는 정렬 방법이다.
원소들 중에 같은 값이 있는 경우 같은 값들의 정렬 이후 순서가 초기 순서와 달라질 수 있어 불안정 정렬에 속한다.
장점
- 속도가 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.(퀵 정렬은 O(logn)만큼 메모리를 필요로 한다.)
단점
- 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
분할 정복(Divide And Qunquer) 방법
1. 리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
2. 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고,
피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 나눈다.
이렇게 리스트를 작은 문제로 나누는 것을 분할이라고 한다.
분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
3. 분할된 두 개의 작은 리스트에 대해 재귀적(Recursion)으로 이 과정을 반복한다.
재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
재귀 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지게 된다.
따라서 이 알고리즘은 반드시 끝난다는 것이 보장된다.
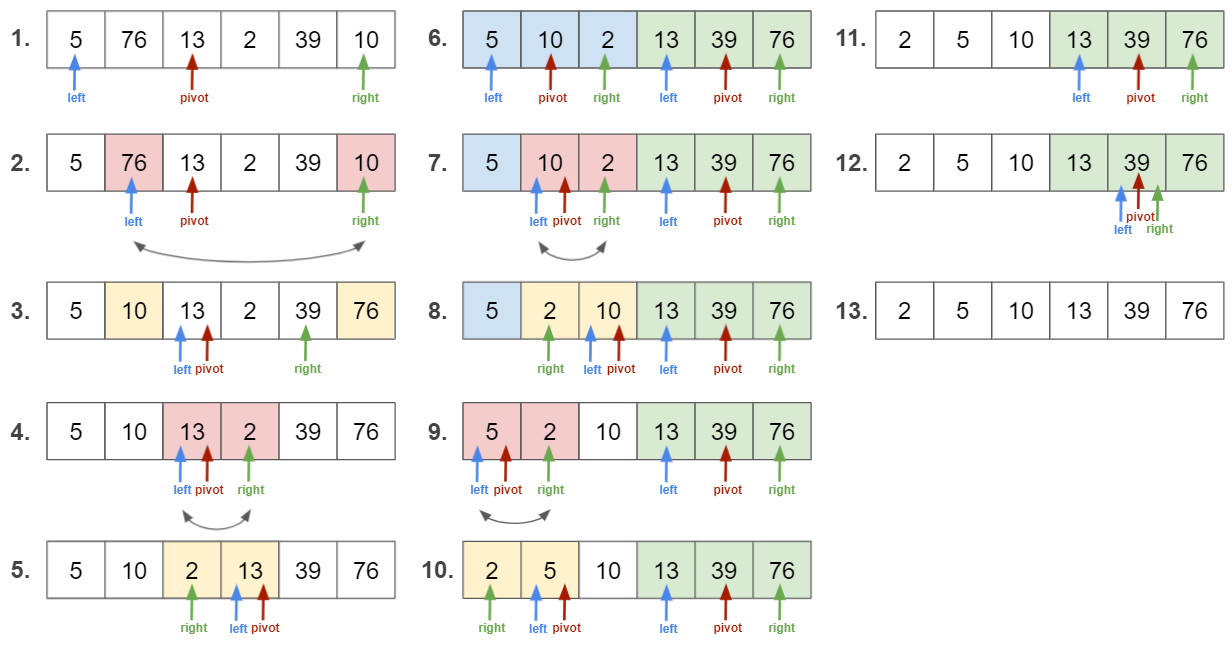
알고리즘 구현
재귀 방식
/**재귀를 활용한 퀵 정렬*/
void quickSort(vector<int> &list, int start,int end){
if(start >= end)
return;
int left = start;
int right = end;
int mid = (start + end) / 2;
int pivot = list[mid];
while(left <= right){
while(list[left] < pivot) left++;
while(list[right] > pivot) right--;
if(left <= right){
swap(list[left++],list[right--]);
}
}
quickSort(list,start,right);
quickSort(list,left,end);
}
반복문 방식
재귀 형식으로 정렬을 하게 되면 메모리 오버플로우가 생겨날 수 있다.
재귀 대신 스택을 활용하면 반복문으로 퀵 정렬을 할 수 있다.
/**반복문과 스택을 활용한 퀵정렬*/
void quickSort(vector<int> &list, int start,int end){
stack<int> s;
s.push(start);
s.push(end);
int left,right,mid,pivot,_start,_end;
while(!s.empty()){
right = s.top();
s.pop();
left = s.top();
s.pop();
_start = left;
_end = right;
mid = (_start + _end) / 2;
pivot = list[mid];
while(left <= right){
while(list[left] < pivot) left++;
while(list[right] > pivot) right--;
if(left <= right){
swap(list[left++],list[right--]);
}
//Left Side List
s.push(_start); //left
s.push(right); //right
//Right Side List
s.push(left); //left
s.push(_end); //right
}
}
}시간 복잡도
- 두 그룹으로 분할하는데 n의 시간이 걸리고 분할된 단계가 log(n) 개 존재하므로 평균 정렬 속도는 O(nlog2 n)
- 분할한 결과가 한쪽으로 몰리는 최악의 경우에는 O(n^2)
'기초 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이진 탐색(Binary Search) (0) | 2021.12.02 |
|---|---|
| [알고리즘] 합병 정렬(Merge Sort) (0) | 2021.11.29 |
| [알고리즘]삽입 정렬(Insertion Sort) (0) | 2021.11.24 |
| [알고리즘] 선택 정렬(Select Sort) (0) | 2021.11.24 |